


Le site bien être
Le site bien être
Le site bien être




































































Le périnée est un groupe de muscles situés entre les jambes et ayant pour fonction …



Les huiles essentielles sont de plus en plus populaires pour leur efficacité et leurs bienfaits …




L’utilisation des pierres pour améliorer notre bien-être physique, mental et émotionnel est une pratique ancienne …



De nos jours, de plus en plus de personnes recherchent des solutions pour améliorer leur …



La douleur chronique est un problème de santé persistant et invalidant qui touche de nombreuses …



La lithothérapie est une méthode de soin holistique qui utilise l’énergie des pierres pour rétablir …



La lithothérapie est une méthode de soin alternatif qui utilise l’énergie des pierres et des …



La lithothérapie est une médecine non conventionnelle qui utilise les énergies vibratoires des pierres pour …



La lithothérapie est une approche alternative de bien-être qui utilise les propriétés énergétiques des pierres …
La lithothérapie est une pratique ancienne qui consiste à utiliser les pierres et cristaux pour …



Les huiles essentielles sont de petits bijoux, qui recèlent pour chacune d’entre elles de grands …



La méditation est une pratique ancienne qui a prouvé sa capacité à favoriser la relaxation, améliorer …



Le yoga et le surf sont deux disciplines qui semblent avoir été créées pour être …



Le desk yoga est une pratique de plus en plus répandue dans les milieux professionnels, …



Les douleurs dorsales et lombaires touchent un grand nombre de personnes aujourd’hui. Le stress, la sédentarité ou …



Salut à tous, chers lecteurs de notre blog yoga! Nous nous retrouvons aujourd’hui sur un …



Le yoga est une discipline ancestrale qui apporte de nombreux bienfaits, tant sur le plan …



La radiofréquence multi-aiguilles est une technique utilisée dans le domaine de la dermatologie et de …



Le chakra sacré ou Svadhisthana représente la créativité et l’expression de soi. Il est relié …



Les différents types de revenus des professeurs de yoga Le salaire moyen d’un professeur de …



L’huile essentielle de tea tree, également connue sous le nom d’arbre à thé, est une …



Si vous êtes passionné par le yoga ou par les enfants et que vous souhaitez …



Le thé est l’une des boissons les plus consommées au monde. Il est à la …



Les Lyonnais peuvent enfin découvrir le yoga, une pratique ancestrale qui aide à retrouver l’équilibre …



La méditation est une pratique millénaire qui a connu des régressions et des renaissances. Au …



Beaucoup d’entre nous ressentent (au minimum) un bourdonnement régulier d’anxiété de faible intensité au fil …



Chaque être humain est différent et pourtant nous partageons tous le besoin fondamental de dormir. …



Qu’est ce qu’un végétarien ? Un végétarien est une personne qui ne consomme pas de …



Le marché européen du CBD est en plein essor, mais les consommateurs savent-ils vraiment ce …



Aujourd’hui, le yoga nu est de plus en plus pratiqué, que ce soit par les …



Les huiles de CBD ont le vent en poupe. Le marché est actuellement très vaste …



Si vous êtes sensible au bruit, cet article est fait pour vous. Nous parlerons de …



De plus en plus de personnes découvrent les bienfaits du yoga et ses effets positifs …



Vous vous êtes toujours demandé quels étaient les bienfaits du yoga pour les débutants ? …



Vous recherchez une manière simple et relaxante de commencer à pratiquer le yoga ? Vous …



Vous et votre partenaire êtes-vous à la recherche d’une nouvelle façon de faire du yoga …



Le yoga est une discipline ancienne qui a été pratiquée pendant des siècles. Grâce à …



Le Centre de Bien-être en Ligne offre une variété de services qui peuvent vous aider …



Vous cherchez une manière pratique et accessible de faire du yoga ? Les studios de …



Créer le meilleur studio vidéo de yoga pour votre entreprise peut sembler être une tâche …



De nombreux préceptes « bien-être » pour se sentir mieux au quotidien sont apparus au …



Ce n’est pas pour rien que le yoga existe depuis des milliers d’années : c’est …



Les produits alimentaires à base de cannabidiol ont de plus en plus de succès. Il …



On aimerait bien vous faire part de notre avis sur Happyngood, qui propose divers accompagnements …



La sophrologie est une méthode de relaxation qui permet de mieux gérer son stress et …



La sophrologie est une pratique qui gagne de plus en plus d’adeptes en France. Si …



Il y a quelques années, la sophrologie était presque inconnue du grand public. Aujourd’hui, elle …



Extraites de la plante du chanvre (ou cannabis), les fleurs de CBD sont tout simplement …



Le yoga est une pratique ancestrale qui a de nombreux bienfaits sur la santé. L’ouverture …



Le yoga est une excellente activité pour prévenir ou soulager les douleurs du dos. En …



Le yoga est une pratique ancienne qui présente de nombreux bienfaits pour la santé. En …



Le yoga est une pratique ancienne qui est devenue extrêmement populaire ces dernières années. Les …
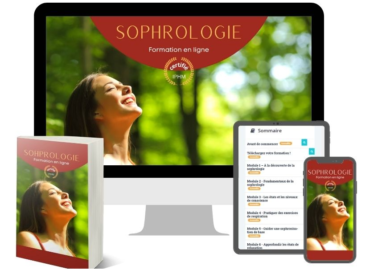


Comment devenir sophrologue est la question qui vous intrigue, et vous n’êtes pas seul(e). Aujourd’hui, …



Que ce soit pour approfondir ses connaissances personnelles, élargir ses compétences, ou se reconvertir, de …



Les formations à distance sont de plus en plus plébiscitées. En effet, elles permettent de …



Selon le Bulletin de l’OMS (Organisation Mondiale de la Santé) les remèdes traditionnels séduisent de …



Le secteur de la formation en ligne a explosé depuis 2000, avec une croissance de …



De plus en plus de Français souhaitent pratiquer régulièrement une activité physique. Et la majorité …



L’argile verte est également connue sous le nom d’argile géothermique. C’est un type de sédiment …



L’art-thérapie fait de plus en plus parler d’elle ces dernières années. Mais malgré cet engouement, …